
As a math teacher I had never given any thought to the concept of teaching digital root until I ran across Kim Sutton’s book Power of Digital Root: 10 Lessons For Understanding. Kim Sutton, if you are not familiar, runs Creative Mathematics (mentioned on my Recommended Resources page) and is one of my favorite math gurus. I worked through the lessons in her book with a small group of gifted/talented second/third graders I was tutoring. They were fascinated by it and enjoyed finding the digital roots of large numbers. They also enjoyed seeing how figuring digital root helped them check work in all operations. Since then I have included these lessons in math instruction with elementary children at any level, and found it helpful to all of them. The book is written for 2nd-6th grade students and includes data sheets, activities, and games.
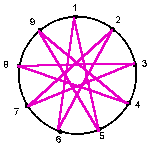
I also found this fun lesson from Teaching Ideas using multiplication facts and the digital roots of their products to create visual art patterns. I loved this lesson as it not only taught digital root but practiced multiplication and reinforced the idea that math is all about patterns.
Here is an example of the pattern created by the digital roots of the 4 and 5 times tables.
What Is Digital Root?
In short, to find the digital root of a number, simply add all its digits. If the sum is more than 9, add the digits again. The single digit obtained at the end is the digital root of the number.
Nrichmaths has this article on digital roots for elementary/middle school students.
Songs For Teaching has a digital root song on their Intell-Tunes Divisibility Rules CD. You can see the lyrics here.
If you would like a in depth mathematical explanation about why digital roots are useful for checking operations, read this article The Math Behind Using Digital Roots to Check Your Arithmetic.
Checking Operations Using Digital Root
You can check your answers to addition, subtraction, and multiplication problems using digital root. Divisibility rules also require digital root. Nancy Foote has YouTube videos explaining all of these which I have embedded below. However, I highly recommend Kim Sutton’s book for teaching these concepts step by step with fun activities and games to help students practice.
Checking Addition With Digital Root
The sum of the digital root of the addends is the same as the digital root of the sum.
Checking Subtraction With Digital Root
The digital root of a difference is the difference of the digital roots of the numbers in the subtraction problem.
Checking Multiplication Using Digital Root
Divisibility Rules Using Digital Root
The divisibility rules that use digital root are:
- Divisibility rule for 3 If the digital root of the number is divisible by 3, then the number is divisible by 3.
- Divisibility rule for 9. The rule for division by 9 is similar to the rule for division by 3: If the digital root of the number is divisible by 9, then the number itself is divisible by 9. The rule for calculating the remainder is even simpler: if the digital root is not 9, then the remainder of division by 9 is just the digital root itself!
Vedic Math
While researching this article, I ran across the application of digital root in Vedic Math, a form of Indian mathematics. This method uses digital root for higher level math calculations including finding square roots, algebra, geometry, and calculus.
The Vedic square replaces the products in a 9*9 multiplication chart with the digital roots of the products, creating a pattern called the Vedic square. As Wikipedia says, “Numerous geometric patterns and symmetries can be observed in a Vedic square some of which can be found in traditional Islamic art.”
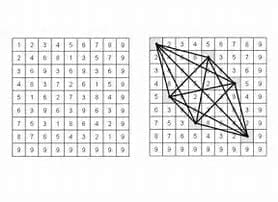
Vedic math, based on the square, is used to quickly make mental calculations. You can learn more about it at Mathlearners.com: What Is Vedic Mathematics and How Vedic Maths Is Important.
Similarly, Trachtenberg Speed Math uses digital root.
